지난 글에서 사이즈 피쳐가 무엇인지 기본 개념을 알아봤다면, 이번에는 좀 더 구체적으로 들어가 보자. 어떤 형상이 사이즈 피쳐가 되려면 반드시 만족해야 하는 두 가지 조건이 있다. 이 조건들을 정확히 이해해야 실제 도면에서 사이즈 피쳐를 제대로 구분할 수 있다.
첫 번째 조건: 사이즈 공차가 반드시 있어야 한다.
사이즈 피쳐가 되기 위한 첫 번째 조건은 사이즈 공차가 정의되어 있어야 한다는 것이다. 이게 생각보다 중요한 포인트다. 현장에서 일하다 보면 이런 경우를 자주 본다. 도면에 원형 구멍이 그려져 있고, 그 옆에 ‘∅20'이라고 적혀있다. 언뜻 보면 사이즈 피쳐 같지만, 실제로는 그렇지 않다. 왜냐하면 공차가 없기 때문이다.
진짜 사이즈 피쳐가 되려면 '∅20±0.1' 또는 '∅20+0.2/-0.1' 같이 사이즈 공차가 명시되어 있어야 한다. 단순히 숫자만 적혀있다면 그건 단순한 정보용 표기일 뿐이다. 베이직 치수일 수도 있고, 참고 치수일 수도 있다. 이는 형상의 크기에 대한 정보만 나타낼 뿐이다.
이런 구분이 중요한 이유는 공차가 있어야만 실제로 '이 정도 범위 안에서 만들어도 된다'는 기준이 생기고, 그 기준을 활용할 수 있기 때문이다.
두 번째 조건: 대응점이 존재해야 한다.
사이즈 공차가 있다고 해서 무조건 사이즈 피쳐가 되는 건 아니다. 두 번째 조건인 '대응점의 존재'도 만족해야 한다. 대응점이란 쉽게 말해 '서로 마주보는 점들'을 뜻한다. 원형 구멍을 생각해보자. 구멍의 한쪽 벽면에 있는 점과 정반대편 벽면에 있는 점이 대응점이다. 이 두 점 사이의 거리가 바로 그 구멍의 직경이 된다. 그런데 모든 형상이 대응점을 가지는 건 아니다. 이는 뒤에서 자세히 살펴본다.
캘리퍼로 간단하게 판별하는 방법
대응점이 있는지 없는지 판별하는 가장 쉬운 방법이 있다. 바로 버니어 캘리퍼를 이용하는 것이다.
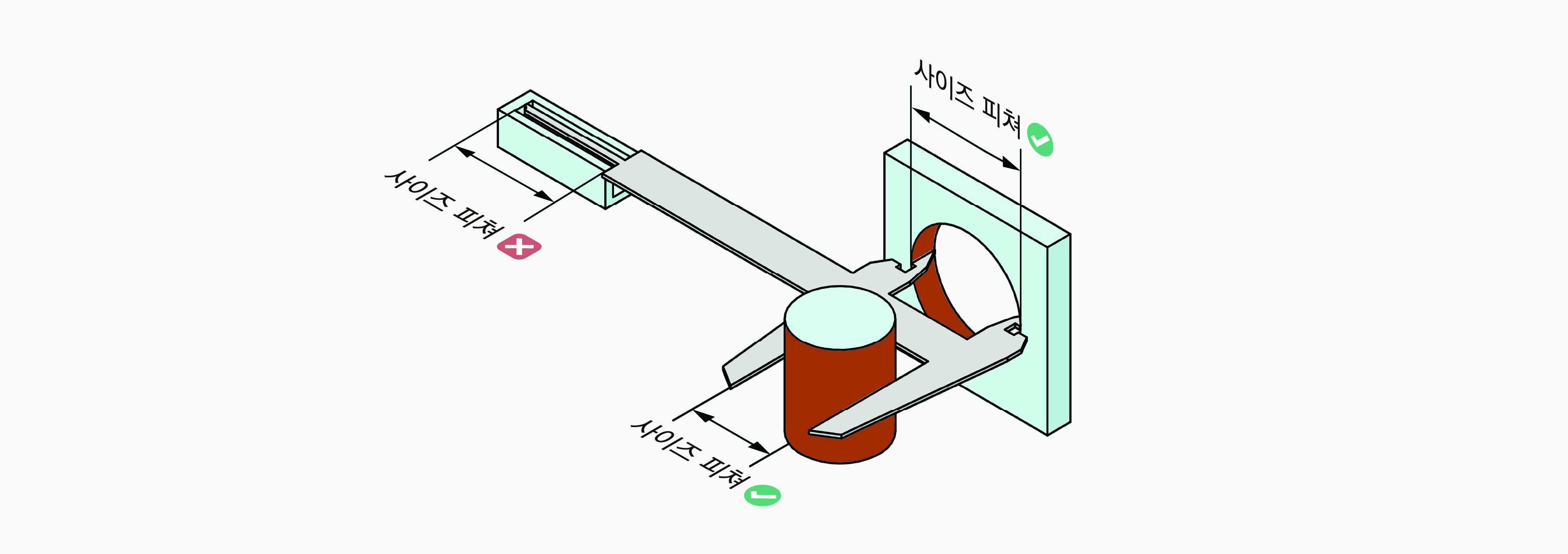
캘리퍼에는 두 가지 측정 부위가 있다. 하나는 바깥쪽을 재는 부분(외경용)이고, 다른 하나는 안쪽을 재는 부분(내경용)이다. 만약 어떤 형상을 캘리퍼의 상단 집게로 잴 수 있다면, 그 형상은 대응점을 가지고 있다는 뜻이다.

외피쳐의 경우를 보자. 원통형 축이나 사각형 돌출부 같은 것들은 캘리퍼의 바깥쪽 측정 집게로 잴 수 있다. 축의 한쪽 면과 반대쪽 면을 캘리퍼로 집어서 직경이나 너비를 측정할 수 있다.

내피쳐는 반대다. 원형 구멍이나 사각형 홈 같은 것들은 캘리퍼의 안쪽 측정 부위를 구멍 안에 넣어서 내부 사이즈를 잴 수 있다. 구멍의 한쪽 벽과 반대쪽 벽 사이의 거리를 측정하는 것이다.
하지만 캘리퍼의 상단 집게로 측정할 수 없는 치수들도 있다. 예를 들어 어떤 표면에서 다른 표면까지의 거리나 높이 같은 것들 말이다. 이런 치수들은 캘리퍼의 깊이 측정용 끝부분을 사용하거나 다른 측정 도구를 써야 한다. 이런 경우는 대응점이 없으므로 사이즈 피쳐가 아니다.
사이즈 치수와 다른 치수들의 구분
여기서 중요한 개념 하나를 짚고 넘어가야 한다. GD&T에서는 치수를 크게 세 종류로 나눈다. 크기 치수, 위치 치수, 각도 치수가 그것이다.
크기 치수는 물체 자체의 크기를 나타내는 치수다. 구멍의 지름, 축의 지름, 판의 두께 같은 것들이다. 이런 치수들만 사이즈 피쳐가 될 수 있고, 치수공차를 적용할 수 있다. 위치 치수는 한 피쳐에서 다른 피쳐까지의 거리를 나타낸다. 예를 들어 구멍의 중심에서 모서리까지의 거리 같은 것들이다. 이런 치수들은 대응점이 없으므로 사이즈 피쳐가 아니다. 각도 치수도 마찬가지다. 두 면 사이의 각도나 기울기 같은 것들은 대응점의 개념이 적용되지 않는다.
여기서 중요한 규칙이 하나 있다. GD&T를 제대로 적용한다면, 크기 치수에만 치수공차를 사용해야 한다. 위치 치수나 각도 치수에는 기하공차를 사용해야 한다. 하지만 현실에서는 이 규칙을 지키지 않는 도면들을 자주 볼 수 있다. 위치를 나타내는 치수에 ±공차를 붙여놓은 경우들 말이다. 엄밀하게 말하면 이런 도면은 GD&T 원칙에 맞지 않는다.
호형 피쳐의 특별한 경우
호(arc) 형태의 피쳐는 특별히 주의해야 한다. 호의 각도에 따라 사이즈 피쳐가 될 수도 있고 아닐 수도 있기 때문이다.
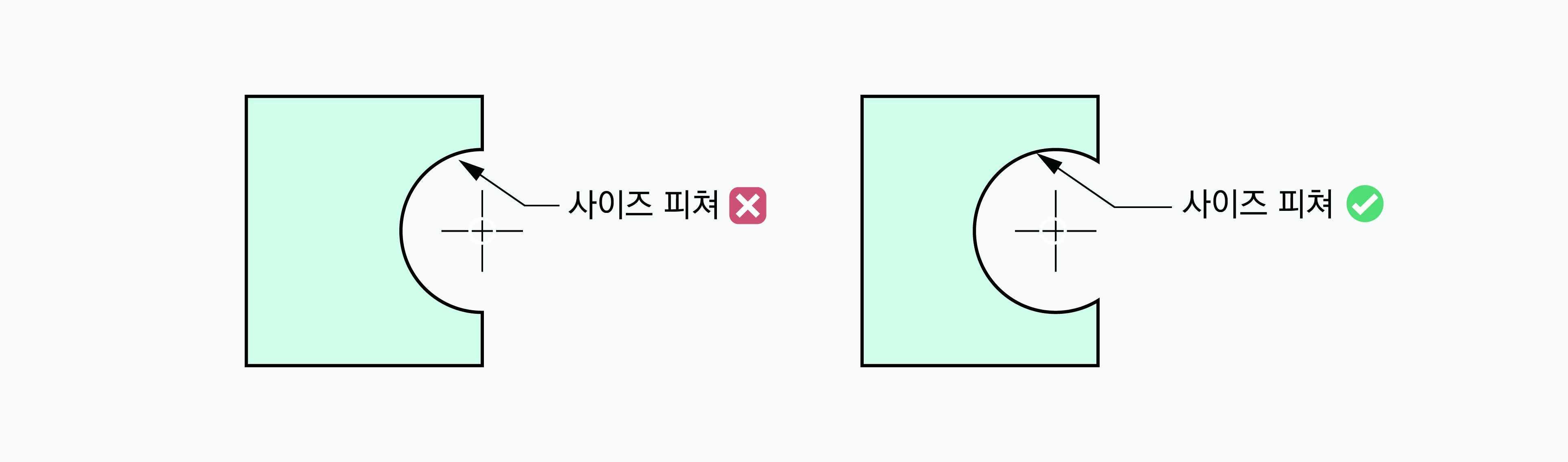
왼쪽 그림과 같이 호가 180°보다 작아지면, 이런 호에서는 서로 마주보는 점이 없다. 호의 한쪽 끝에서 다른 쪽 끝까지는 대응점이라고 할 수 없다. 왜냐하면 호의 중심을 지나는 직선상에 있지 않기 때문이다. 따라서 아무리 사이즈 공차를 명시해도 사이즈 피쳐가 될 수 없다.
반면 180° 이상의 호는 다르다. 반원 이상이 되면 직경 방향으로 서로 마주보는 점들이 생긴다. 이런 점들은 진짜 대응점이라고 할 수 있고, 캘리퍼로 측정이 가능하다. 물론 이 경우에도 실제로 사이즈 피쳐가 되려면 사이즈 공차가 함께 정의되어야 한다.
예를 들어 270° 호가 있다고 해보자. 이 호에서는 지름 방향으로 서로 마주보는 여러 쌍의 점들이 존재한다. 따라서 이 호에 크기 공차를 정의하면 사이즈 피쳐가 될 수 있다.
실제 도면에서 판별하는 방법
실무에서 도면을 볼 때 사이즈 피쳐인지 아닌지 빠르게 판별하는 체크리스트가 있다.
- 크기 공차가 있는지 확인한다. ±기호나 상하한 공차가 명시되어 있어야 한다. 베이직 치수나 참고 치수로 표시되어 있다면 사이즈 피쳐가 아니다.
- 대응점이 있는지 생각해본다. 캘리퍼로 측정할 수 있는 형상인지 머릿속으로 그려본다. 바깥쪽 집게든 안쪽 집게든 상관없이 캘리퍼로 잴 수 있다면 대응점이 있는 것이다.
- 치수가 를 나타내는지 확인한다. 위치나 거리, 각도를 나타내는 치수라면 사이즈 피쳐가 아니다.
이 세 가지 조건을 모두 만족해야만 진짜 사이즈 피쳐라고 할 수 있다.
잘못 적용된 도면의 예
현장에서 자주 보는 잘못된 예를 하나 들어보자. 어떤 도면에 두 구멍 사이의 거리가 '50±0.2'로 표시되어 있다고 하자. 언뜻 보면 치수공차가 있으니까 문제없어 보인다. 하지만 이건 잘못된 표기다. 두 구멍 사이의 거리는 위치 치수이지 크기 치수가 아니기 때문이다. 이런 경우에는 베이직 치수로 거리를 정의하고, 위치공차나 윤곽공차 같은 기하공차를 사용해야 맞다.
이런 실수가 생기는 이유는 전통적인 치수 공차 방식에 익숙한 사람들이 GD&T를 제대로 이해하지 못했기 때문이다. GD&T에서는 각각의 치수 유형에 맞는 공차를 사용해야 한다는 원칙을 지켜야 한다.
마무리
사이즈 피쳐가 되기 위한 두 가지 조건을 정리해보자.
- 첫째, 반드시 사이즈 공차가 정의되어 있어야 한다.
- 둘째, 대응점이 존재해야 한다.
이 두 조건을 정확히 이해하면 실제 도면에서 사이즈 피쳐를 구분하는 데 큰 도움이 된다. 또한 GD&T의 다른 개념들을 배울 때도 훨씬 수월해진다. 특히 캘리퍼를 이용한 판별법은 현장에서 매우 실용적이다. 복잡한 이론을 외울 필요 없이, 단순히 '캘리퍼로 잴 수 있나?'를 생각해보면 된다. 다음에는 사이즈 피쳐의 핵심 개념인 MMC와 LMC에 대해 알아보겠다. 이 개념들을 이해하면 GD&T의 진짜 위력을 느낄 수 있을 것이다.
'기하공차 기초' 카테고리의 다른 글
| 기초 #09 피쳐의 이해 2 : 서피스와 피쳐 (4) | 2024.11.12 |
|---|---|
| 기초 #08 Rule #1 : ASME Y14.5에서 가장 중요하고 기본이 되는 원칙 (5) | 2024.11.12 |
| 기초 #06 사이즈 피쳐의 이해 1 : 사이즈 피쳐의 기본 개념과 특징 (0) | 2024.11.12 |
| 기초 #05 기하공차는 기하학적 속성 4가지를 통제한다. (0) | 2024.11.12 |
| 기초 #04 피쳐의 이해 1 : 피쳐란 무엇인가? (3) | 2024.11.12 |





