초급 #14 6자유도란?
데이텀과 DRF를 이해하려면 먼저 6자유도를 이해해야 한다. 왜냐하면 데이텀과 DRF의 핵심적인 역할이 바로 이 6자유도를 제한하는 것이기 때문이다.
우리가 일상에서 접하는 모든 물체는 3차원 공간에 존재한다. 책상 위에 놓인 스마트폰을 생각해보라. 이 스마트폰이 공간상에서 어떤 상태로 있는지 설명하려면, 단순히 "책상 위에 있다"라고 말하는 것으로는 부족하다. 스마트폰의 상태를 완전하게 설명하려면 더 정확하고 체계적인 방법이 필요하다. 바로 이 때 6자유도 개념이 등장한다. 3차원 공간에서 물체의 위치와 자세를 완전히 설명하려면 6개 방향의 움직임을 모두 설명해야 하는데 이를 6자유도라고 부른다.
책상 위에 있는 스마트폰이 어떻게 움직일 수 있는지 생각해보자.

병진자유도 : 3개의 직선이동
스마트폰을 책상 위에서 좌우로 밀어보자.

다음으로 앞뒤로 밀어보자.

마지막으로 책상 위로 들어올려보자. 그리고 책상 아래로 내려보자.
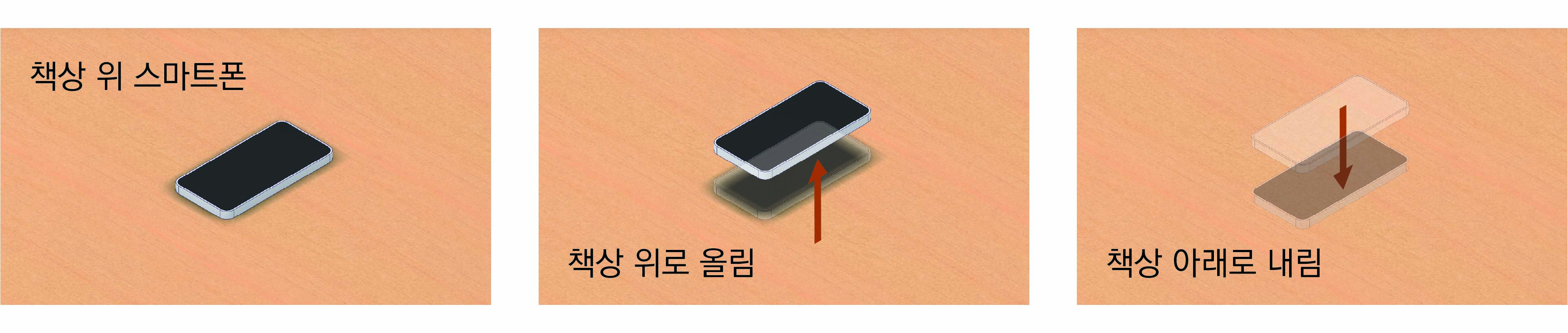
이렇게 3차원 공간에서 스마트폰은 세 방향으로 직선이동이 가능하다. 이것이 병진자유도 3개다. 이 세 방향을 보통 x방향, y방향, z방향으로 표현한다. 구체적인 방향은 중요하지 않다. x, y, z는 이름일 뿐이다. 중요한 것은 서로 수직하다는 것이다. 서로 수직하는 세 방향으로 구분하기만 하면 된다. 3차원 공간에서 물체의 상태 중 위치를 3개의 병진자유도에 의한 위치로 설명할 수 있다.
병진자유도는 생각하기가 쉽다. 어떤 점이 3차원 좌표계 위에서 앞뒤로, 좌우로, 위아래로 움직일 수 있다고 상상하면 된다. 하지만 현실에서 물체는 점이 아니라 입체로 존재한다. 따라서 직선이동만으로는 물체의 운동을 완전히 설명할 수 없다. 어떤 점이 (0,0,0)에 위치한다고 해도 여전히 여러 가지 자세를 취할 수 있다.
회전자유도 : 3개의 회전이동
스마트폰을 책상 위에서 회전시켜보자.
이 때 스마트폰의 오른쪽 모서리를 (0,0,0)으로 보고 오른쪽 모서리를 고정한 상태에서 회전시켜보자.

다음으로 좌우로 기울여보자.

마지막으로 앞뒤로 기울여보자.

이렇게 3차원 공간에서 스마트폰은 세 방향으로 회전이동이 가능하다. 이것인 회전자유도 3개다. 이 세 방향을 u방향, v방향, w방향으로 표현한다. 병진자유도와 마찬가지로 구체적인 방향은 중요하지 않다. u, v, w는 이름일 뿐이다. 중요한 것은 회전중심축이 서로 수직하다는 것이다. 서로 수직하는 세 방향으로 구분하기만 하면 된다. 항공기에서는 이를 롤링, 피칭, 요잉이라고 한다. 이렇게 3개의 회전자유도에 의한 자세까지 설명하면 3차원 공간에서 물체의 상태는 완전히 설명된다.
책상 위 스마트폰의 자유도 제한
이처럼 스마트폰은 3차원 공간에서 6개 방향으로 움직일 수 있다. 하지만 스마트폰을 책상 위에 놓은 상태, 즉, 스마트폰 뒷면과 책상 상면이 맞닿은 상태에서는 움직일 수 없는 방향이 있다.

먼저 스마트폰은 책상 아래로 내려갈 수 없다. 스마트폰이 책상을 뚫고 내려갈 수 없기 때문에 책상 위 스마트폰을 책상 아래로 내릴 수 없다. 다음으로 스마트폰 뒷면과 책상 상면이 맞닿은 상태에서는 스마트폰을 좌우로 회전할 수 없다. 마찬가지로 앞뒤로도 회전할 수 없다.
스마트폰과 책상이 맞닿으면, 스마트폰은 책상 아래로 내려갈 수 없어 병진자유도 1개를 잃고, 스마트폰은 좌우로, 앞뒤로 회전할 수 없기 때문에 회전자유도 2개를 잃는다. 이것이 책상이 자유도를 제한하는 것이고, 스마트폰 자유도가 제한되는 것이다.
마치며
3차원 물체인 스마트폰은 3차원 공간에서 6개 방향으로 움직일 수 있어 이를 6자유도를 가진다라고 말한다. 하지만 스마트폰을 책상에 놓는 순간 스마트폰은 책상과의 접촉에 의해 6개의 자유도 중 3개를 잃는다. 이처럼 3차원 입체가 3차원 공간과 관계를 맺으면, 그 관계에 의해 3차원 입체는 3차원 공간에서 자유도 일부 또는 전부를 잃으면서 구속된다.
이제 3차원 입체는 6자유도를 가지고 있고, 이를 3차원 공간에 놓으면 가지고 있던 자유도의 일부를 잃는다는 것까지 이해했다. 이제 기하공차로 돌아가서 자유도를 잃는다는 것이 어떤 의미인지 자세히 살펴보자.

